Τα μαθηματικά και η μουσική είναι δύο τέχνες-επιστήμες που έχουν κοινή μήτρα, δύο γλώσσες με τις οποίες μπορούν να συνεννοηθούν και να επικοινωνήσουν οι άνθρωποι μεταξύ τους. Επιπλέον, τα μαθηματικά δεν είναι μόνο επιστήμη αλλά και τέχνη, ενώ η μουσική δεν είναι μόνο τέχνη αλλά και επιστήμη. Άλλωστε, όλες οι μορφές τέχνης εμπεριέχουν και αντίστοιχες μορφές επιστήμης, με τις οποίες αλληλοπροσδιορίζονται συνειδητά ή ασύνειδα. Τις τελευταίες δεκαετίες η μελέτη των καθολικών στοιχείων, που εισήγαγε ο κορυφαίος γλωσσολόγος, μαθηματικός και φιλόσοφος Νόαμ Τσόμσκι και αφορούν τη γλώσσα, έχει μπει δυναμικά και στη μελέτη της μουσικής, μιας και καθολικά στοιχεία ανιχνεύονται στις μουσικές όλων των λαών. Η μελέτη των στοιχείων εκείνων δηλαδή που κάθε άνθρωπος μπορεί να αναγνωρίσει και να νιώσει, ανεξάρτητα από την εποχή και τον τόπο που μεγάλωσε, και τα οποία είναι κοινά και παραμένουν αναλλοίωτα στον χώρο και τον χρόνο. Από την πεντατονία μέχρι την επαναληπτικότητα μουσικών ρυθμών που οδηγούν σε πανανθρώπινα συναισθήματα.
Αρχή
Η μουσική και τα μαθηματικά είναι δύο από τις αρχαιότερες τέχνες-επιστήμες του κόσμου, συνυφασμένες με τη φύση του ανθρώπου. Πεποίθησή μας είναι ότι τέχνη και επιστήμη αποτελούν δύο εκφάνσεις του ίδιου φαινομένου, αλληλοεξαρτώνται, αλληλοσυμπληρώνονται, ενυπάρχουν η μία στην άλλη. Επιπλέον, θα μπορούσαμε να ισχυριστούμε ότι είναι δύο γλώσσες παγκόσμιες με τις οποίες μπορούν να επικοινωνήσουν οι άνθρωποι μεταξύ τους.
Παρακάτω θα προσπαθήσουμε να εξηγήσουμε πώς αντιλαμβανόμαστε αυτές τις έννοιες –τέχνη, επιστήμη, γλώσσα– και πώς αυτές εμπλέκονται και αλληλοεξαρτώνται.
Καταρχήν, όσον αφορά την τέχνη και την επιστήμη και πιο συγκεκριμένα τα μαθηματικά, είναι γνωστό ότι βασικό στοιχείο της τέχνης και της δημιουργίας θεωρείται η έμπνευση, αλλά αυτό που ίσως ο πολύς κόσμος δεν έχει απολύτως συνειδητοποιήσει, είναι ότι η έμπνευση αποτελεί ένα από τα βασικότερα στοιχεία της επιστήμης συμπεριλαμβανομένων και των μαθηματικών. Τα μαθηματικά συνήθως προβάλλονται ως μία και μοναδική «τετράγωνη» λογική, προβάλλονται ως οι de jure φορείς και τιμητές της αλήθειας και της «αντικειμενικότητας». Όμως, οι μαθηματικοί, τουλάχιστον οι περισσότεροι, γνωρίζουμε ότι κάτι τέτοιο δεν ισχύει και δεν πρέπει να ισχύει. Και αυτό γιατί γνωρίζουμε ότι όλες οι μαθηματικές θεωρίες ξεκινούν από ένα «έστω», ένα μαγικό «έστω», που είχε την έμπνευση ο εκάστοτε μαθηματικός να σκεφτεί και να χτίσει έναν ολόκληρο κόσμο πάνω σε αυτό. Όπως έχτισε την ευκλείδεια γεωμετρία ο Ευκλείδης με τρία αξιώματα που έθεσε ο ίδιος. Σε άλλους χώρους και σε άλλους χρόνους όμως, χρησιμοποιούνται εντελώς διαφορετικά αξιώματα. Αυτό, λοιπόν, το «έστω» είναι μία σύμβαση, μία συμφωνία με τον συνομιλητή-δέκτη μας και όχι μία «αντικειμενική αλήθεια» που επιβάλλεται από τους νόμους της φύσης. Έτσι, λοιπόν, στα μαθηματικά όταν μιλάμε για έμπνευση, δεν εννοούμε απλά την έμπνευση της ιδέας του πώς να λύσουμε ένα πρόβλημα, αλλά την έμπνευση ώστε να δημιουργήσουμε έναν εντελώς καινούργιο κόσμο, ο οποίος στην αρχή μπορεί να φαντάζει απλά σαν ένα παιχνίδι ή ακόμα και σαν άσκηση του μυαλού, αλλά στο τέλος μπορεί να εξηγήσει φυσικά φαινόμενα, που μέχρι τότε δεν μπορούσαν να εξηγηθούν. Δηλαδή κάτι που στην αρχή φαίνεται απλώς μια θεωρία, να γίνεται τελικά εφαρμογή. Να περνάει δηλαδή το στενών ανθρώπινων κριτηρίων «τεστ», που θέτουν ως απαράβατη προϋπόθεση ότι, για να είναι κάτι «σωστό», θα πρέπει να επαληθεύεται και στην πράξη. Στην τέχνη όμως πολλές φορές έχουμε δει ότι ένα έργο τέχνης μπορεί να είναι πιο τολμηρό ή προχωρημένο από την εποχή του, αβάν γκαρντ (avant garde), και έτσι να έρχεται η αναγνώρισή του από το πλατύ κοινό μετά από πολλές δεκαετίες. Το ίδιο συμβαίνει και με την «τέχνη», την επιστήμη των μαθηματικών και όχι μόνο.
Σε αυτό το σημείο, θα προσπαθήσουμε να αναδείξουμε το γεγονός ότι η μουσική και τα μαθηματικά είναι δύο γλώσσες και μάλιστα παγκόσμιες, ξεκινώντας με κάποιους ορισμούς της γλώσσας.
Μερικοί ορισμοί της γλώσσας
Θα πρέπει να τονίσουμε ότι, όπως συμβαίνει και με τις άλλες επιστήμες, ο απόλυτος καθορισμός του αντικειμένου δεν είναι εφικτός. Ένας κλασικός ορισμός είναι αυτός του Chomsky:
Γενικά, η αξία της προσπάθειας για καθορισμό έγκειται στο ότι «δίνουν (οι προσπάθειες) τη δυνατότητα να κάνουμε πιο συγκεκριμένες τις υποθέσεις μας, να τις ελέγξουμε και ενδεχομένως να τις αλλάξουμε. Δηλαδή, προσπάθεια για ορισμό είναι απαραίτητη σα βάση για παραπέρα συζήτηση» (Πετρούνιας, 2001: 42). Έτσι, υπάρχουν για παράδειγμα ορισμοί βραχυλογικοί που είναι και οι πλέον ανώδυνοι, επειδή βασίζονται στη βασική αρχή «όσο λιγότερα, τόσο καλύτερα» και κατά συνέπεια δεν επιτρέπουν να φανεί η όποια επιστημονική τοποθέτηση αφήνοντας τον ερευνητή στο απυρόβλητο, μιας και δεν επιδέχονται ιδιαίτερης κριτικής.
«Γλώσσα είναι ένα σύστημα φωνητικών συμβόλων που χρησιμεύουν στην επικοινωνία». Ο ορισμός αυτός είναι γενικός και δεν δίνει λαβή για πολλές αντιρρήσεις. Όμως, μέσα στη γενικότητά του εμπεριέχει τέσσερις βασικές αρχές:
(i) η γλώσσα πραγματώνεται με τη φωνή (φωνητικά σύμβολα), έχει δηλαδή προφορά
(ii) οι ήχοι (φθόγγοι) που παράγονται δεν σημαίνουν τίποτα οι ίδιοι, αλλά συμβολίζουν κάτι άλλο. Επομένως, μία κραυγή πόνου ή ένα γουργούρισμα ικανοποίησης, που εκφράζουν άμεσα το σχετικό ερέθισμα, δεν θεωρούνται μέρος της γλώσσας
(iii) οι φθόγγοι που αρθρώνουμε δεν είναι ανεξάρτητοι, αλλά αποτελούν σύστημα
(iv) σκοπός της γλώσσας είναι η επικοινωνία.
Ακόμη, μπορούμε να συναντήσουμε μεσαίου μεγέθους ορισμούς: «Γλώσσα είναι ένα σύστημα αυθαίρετων φωνητικών συμβόλων που χρησιμεύουν για την ανθρώπινη επικοινωνία» (Πετρούνιας, 2001: 38). Σ’ αυτό τον ορισμό ξαναβρίσκονται οι βασικές αρχές του προηγούμενου ορισμού, καθορίζονται όμως και μερικές ακόμα:
(i) Η προφορά συνεχίζει να θεωρείται πρωταρχικό στοιχείο. Άλλωστε, γλώσσα χωρίς προφορά δεν υπάρχει. Η αποδοχή αυτή είναι πολύ σημαντική, επειδή ανατρέπει προαιώνιες προκαταλήψεις που ήθελαν τη γραφή σημαντικότερη. Πράγματι, μαθαίνει κανείς πρώτα να μιλάει και ύστερα να γράφει και φυσικά κάποιος μπορεί να μιλάει χωρίς να μάθει ποτέ να γράφει. Παρ’ όλα αυτά, τί γίνεται με τις γλώσσες των κωφαλάλων, των τυφλών, τους μορφασμούς, τα σήματα τροχαίας, τα νοήματα, ακόμη και κραυγές ή οσμές, δηλαδή άλλα συστήματα επικοινωνίας συμπεριλαμβανομένων και αυτών των ζώων; Θα πρέπει μάλλον να τα βγάλουμε εκτός αντικειμένου, και αυτό γιατί ο συγκεκριμένος ερευνητής δεν ενδιαφέρεται για τις παραμέτρους «τεχνητά συστήματα επικοινωνίας» ή «ζωικά συστήματα επικοινωνίας».
(ii) Στον ορισμό αυτό επίσης καθορίζεται ότι οι φθόγγοι που προφέρουμε είναι σύμβολα, έχει όμως προστεθεί και ένα νέο στοιχείο: Η άποψη ότι τα σύμβολα αυτά είναι αυθαίρετα. Με άλλα λόγια, η επιλογή είναι αυθαίρετη. Διαφορετικά όλες οι γλώσσες θα είχαν τις ίδιες λέξεις για τις ίδιες έννοιες και δεύτερον δεν θα υπήρχε εξέλιξη γλωσσών: π.χ. η αρχαιοελληνική λέξη «τράπεζα» από τη μια πλευρά εξελίχθηκε στη νεοελληνική «τραπέζι», αλλά επιπλέον η παλιά μορφή της απέκτησε νέα σημασία.
Τέτοιου είδους προβλήματα φαίνεται ότι είχαν απασχολήσει και τους αρχαίους Έλληνες. Για παράδειγμα, ο Αριστοτέλης αντικρούοντας την άποψη του Πλάτωνα που πίστευε ότι οι λέξεις υπάρχουν «φύσει», μίλησε για «κατά συνθήκην λέξεις» και για «σύμβολα». Δηλαδή, υποστήριξε ότι οι λέξεις δεν είναι από τη φύση τους πλασμένες να δηλώνουν αυτό που δηλώνουν, αλλά επειδή έτσι συμφώνησαν οι ομιλητές. Επιπλέον, ο Αριστοτέλης φαίνεται να είχε αντιληφθεί ότι ο προφορικός λόγος υπερτερεί του γραπτού, κάτι ιδιαίτερα σημαντικό για την εποχή, αν λάβει κανείς υπόψη ότι χρειάστηκαν 2.500 χρόνια για να απενοχοποιηθεί ο προφορικός λόγος, αρχικά από τους ιστορικούς γλωσσολόγους και στη συνέχεια από τον Saussure.
(iii) Μία ακόμη σημαντική παρατήρηση στον ορισμό μας είναι το γεγονός ότι η επικοινωνία περιορίζεται σε ανθρώπινη. Χαρακτηρίζοντας τη γλώσσα ως το μέσο της καθαρά ανθρώπινης επικοινωνίας, αποκλείουμε από την έννοια της γλώσσας τη δυνατότητα της επικοινωνίας των ζώων.
Ένας πιο γενικός ορισμός που θα μπορούσαμε να διατυπώσουμε είναι ο εξής: «Γλώσσα είναι ένα σύστημα συμβόλων που χρησιμεύουν στην επικοινωνία» ή και ακόμα γενικότερος: «Γλώσσα είναι ένα σύστημα επικοινωνίας».
Αν δεχτούμε τους παραπάνω ως ορισμούς, όχι μόνο της ανθρώπινης ομιλίας ως πανανθρώπινου φαινομένου, τότε εύκολα μπορούμε να εντάξουμε και τη μουσική αλλά και τα μαθηματικά στην κατηγορία «γλώσσες» και μάλιστα παγκόσμιες, δηλαδή κοινές για όλους τους λαούς, που μπορούν να τις χρησιμοποιούν για να επικοινωνήσουν όλοι οι άνθρωποι μεταξύ τους, ανεξαρτήτως της συγκεκριμένης φυσικής γλώσσας που χρησιμοποιούν ως κοινότητα για να επικοινωνήσουν και η οποία δεν είναι κατανοητή στους ομιλητές άλλων γλωσσών. Αυτό αποτελεί σαφέστατα και το συγκριτικό πλεονέκτημα των μαθηματικών και της μουσικής απέναντι στις φυσικές γλώσσες των κοινοτήτων.
Γλωσσικά καθολικά
Θα προσπαθήσουμε τώρα, έχοντας ως αφετηρία τα γλωσσικά καθολικά, τη μελέτη των οποίων εισήγαγε ο κορυφαίος γλωσσολόγος, μαθηματικός και φιλόσοφος Νόαμ Τσόμσκι (Noam Chomsky) και αφορούν τη γλώσσα, να εξετάσουμε με τη βοήθεια των μαθηματικών τα μουσικά καθολικά στοιχεία που υπάρχουν στις μουσικές των λαών. Τα στοιχεία εκείνα δηλαδή που κάθε άνθρωπος μπορεί να αναγνωρίσει και να νιώσει, ανεξάρτητα από την εποχή και τον τόπο που μεγάλωσε και τα οποία είναι κοινά και παραμένουν αναλλοίωτα στον χώρο και τον χρόνο. Από την πεντατονία μέχρι την επαναληπτικότητα μουσικών ρυθμών που οδηγούν σε πανανθρώπινα συναισθήματα.
Ο Νόαμ Τσόμσκι, δημιουργός –μαζί με τους γλωσσολόγους του περίφημου Τεχνολογικού Ινστιτούτου της Μασαχουσέτης (ΜΙΤ)– της γενετικής- μετασχηματιστικής γραμματικής θεωρεί ότι ο άνθρωπος διαθέτει από τη γέννησή του έναν έμφυτο μηχανισμό, που τον ονομάζει Linguistic Acquisition Device –LAD– ή μηχανισμό γλωσσικής κατάκτησης-απόκτησης. Αυτό το κοινό για όλους εφόδιο υφίσταται μια φυσική και ψυχολογική ωρίμανση, που επιτρέπει στο παιδί να εντοπίσει και να ταυτίσει με τη βοήθεια του περιβάλλοντός του τον τύπο της γλώσσας στον οποίο πρέπει να προσαρμοστεί. Αυτή η υπόθεση για τον έμψυχο χαρακτήρα της γλώσσας οδηγεί λογικά στην επόμενη υπόθεση για τα καθολικά χαρακτηριστικά ή απλώς καθολικά (universals) της γλώσσας.
Πραγματικά, φαίνεται λογική η υπόθεση ότι χωρίς την ύπαρξη αυτών των γλωσσικών καθολικών θα ήταν αδύνατη η εκμάθηση από το παιδί αυτού του ιδιαίτερα περίπλοκου συστήματος που είναι η γλώσσα.
Για τον Νόαμ Τσόμσκι και τους γενετιστές, (γλωσσικά) καθολικά ονομάζονται οι ομοιότητες που υπάρχουν σε όλες τις γλώσσες του κόσμου. Η μελέτη τους αναπτύχθηκε μεταξύ 1960 και 1965 για τις ανάγκες της αυτόματης μετάφρασης από γλώσσα σε γλώσσα. Παρακάτω, παραθέτουμε μερικά παραδείγματα από τον Γκρίνμπεργκ (Greenberg, 1963), όπου μνημονεύονται 45 γλωσσικά καθολικά, και από τον Πετρούνια (2002):
◗ Oι γλώσσες δημιουργούνται υποσυνείδητα μέσα στη γλωσσική κοινότητα με προφορική επικοινωνία.
◗ Οι γλώσσες διαθέτουν προφορά, λεξιλόγιο και συντακτικούς κανόνες. Οι ίδιες είναι ολοκληρωμένα συστήματα και οι επιμέρους τομείς τους αποτελούν επίσης συστήματα.
◗ Μπορεί να υπάρχει διαφορά ανάμεσα στο αφηρημένο γλωσσικό σύστημα που έχει εσωτερικεύσει ο ομιλητής και στη συγκεκριμένη χρήση κάθε φορά.
◗ Το φωνητικό μέρος είναι το υλικό στοιχείο της γλώσσας, αυτό που μπορούμε να ακούσουμε ή να μετρήσουμε. Για όλα τα υπόλοιπα μπορούμε να κάνουμε υποθέσεις και να ελέγξουμε τα συμπεράσματα.
◗ Η σχέση ανάμεσα στη φωνητική μορφή και στη σημασία είναι αυθαίρετη.
◗ Η προφορά στηρίζεται σε αφηρημένες ενότητες, τα φωνήματα, που βρίσκονται σε αντίθεση μεταξύ τους και αποτελούν σύστημα. Ο αριθμός τους είναι μικρός –σπάνια μία γλώσσα διαθέτει περισσότερα από 50– αλλά μπορούν να συνδυαστούν προκειμένου να αποτελέσουν λέξεις. Τα φωνήματα πραγματώνονται στην προφορά με αλλόφωνα (με συγκεκριμένους φθόγγους).
◗ Τα φωνήματα δεν είναι φορείς σημασίας, αλλά διακρίνουν λέξεις με διαφορετική σημασία.
◗ Οποιοδήποτε εκφώνημα σε οποιαδήποτε γλώσσα αποτελείται από υποκείμενο και κατηγόρημα.
◗ Φαίνεται ότι τα σημαντικότερα μέρη του λόγου είναι το όνομα και το ρήμα. Τα ονόματα καθορίζονται με βάση τα δικά τους χαρακτηριστικά (συγκεκριμένο, αφηρημένο, έμψυχο, άψυχο, ανθρώπινο κτλ.), ενώ τα ρήματα καθορίζονται κατά τη σχέση που έχουν προς τα ονόματα: ταιριάζουν με ανθρώπινα, με έμψυχα, με αφηρημένα; Η ενέργειά τους μεταβαίνει σε όνομα; Μεταβαίνει και σε δεύτερο όνομα;
◗ Αν τα ουσιαστικά μιας γλώσσας έχουν γένος, τότε έχουν και οι αντωνυμίες της.
◗ Η σειρά των λέξεων είναι βασική για την κατανόηση του μηνύματος. Τα γραμματικά μορφήματα και ιδιαίτερα τα κλιτικά είναι φορείς συντακτικής λειτουργίας.
◗ Οι γλώσσες κάνουν χρήση τόσο της οικονομίας όσο και του πλεονασμού.
◗ Οι λέξεις αποτελούνται από ένα ή περισσότερα μορφήματα. Τα μορφήματα είναι τα μικρότερα τμήματα λόγου με σημασία ή συντακτική λειτουργία.
◗ Το βασικό λεξιλόγιο είναι περιορισμένο στις 800-1000 λέξεις, με δυνατότητα να αυξηθεί ή να ελαττωθεί ανάλογα με τις κοινωνικές ανάγκες.
◗ Βασική δομή του λόγου είναι η πρόταση. Οι προτάσεις αναλύονται σε φράσεις – ονοματική φράση, ρηματική φράση.
◗ Ο αριθμός των κανόνων θεωρείται πεπερασμένος, όμως ο αριθμός των προτάσεων είναι άπειρος, καθώς άπειροι είναι και οι πιθανοί συνδυασμοί λέξεων.
◗ Τα παιδιά αρχίζουν να αναπτύσσουν τη γλωσσική ικανότητα παράγοντας πρώτα προτάσεις της μίας λέξης, ύστερα των δύο λέξεων και στη συνέχεια αυξάνουν τη συντακτική περιπλοκότητα των προτάσεών τους, περιορίζοντας έτσι την πολυσημία στην προσπάθεια να γίνουν κατανοητά.
◗ Για το μικρό παιδί δεν έχει καμία απολύτως σημασία σε ποιον τύπο γλώσσας ανήκει η δική του.
◗ Τα μικρά παιδιά είναι σύντομα σε θέση να ανασυνδυάζουν τις λέξεις και να παράγουν δικές τους καινούργιες προτάσεις. Με άλλα λόγια, παρουσιάζουν παραγωγικότητα. Επίσης προσπαθούν να εξομαλύνουν τη γλώσσα, δηλαδή να δώσουν ευρύτερη ισχύ στους κανόνες. Ανάλογες διαδικασίες ενεργοποιούνται και στην εκμάθηση της ξένης γλώσσας.
Οπωσδήποτε όλες αυτές οι θεωρίες δεν είναι καινούργιες. Άλλωστε και ο ίδιος ο Τσόμσκι δέχεται τον Αριστοτέλη ως δάσκαλό του και στις θεωρίες του μιλάει για μετασχηματισμούς, δηλαδή για εξέλιξη που βασίζεται και πατάει στα προηγούμενα. Να σημειωθεί ότι ο Αριστοτέλης είχε αναφερθεί στα κοινά χαρακτηριστικά των γλωσσών, ενώ το 1630 ο Γερμανός φιλόσοφος Γιόχαν Άλστεντ (Johann Alsted) χρησιμοποίησε τον όρο γενική γραμματική, που αργότερα χρησιμοποιεί ο Τσόμσκι ως γενική γενετική γραμματική (General Generative Grammar) σε αντιπαράθεση με την ειδική γραμματική, προκειμένου να υποστηρίξει την άποψή του για την ανακάλυψη στοιχείων που σχετίζονται με τη μέθοδο και την αιτιολογία των γραμματικών εννοιών, που είναι κοινές σε όλες τις γλώσσες.
Έτσι διαρκώς εμφανίζονται θεωρίες που μετασχηματίζουν αυτή τη γνώση εμπνεόμενες από νέα πορίσματα της επιστήμης. Σ’ αυτό το πλαίσιο κινείται η πρόταση των Βουγιουκλή και Καμπάκη για ένα γενικό μαθηματικό μοντέλο (πρότυπο) το οποίο εφαρμόζεται σχεδόν σε όλους τους κλάδους των μαθηματικών. Το πρότυπο αυτό βασίζεται στον κλάδο των μαθηματικών που ονομάζεται γραμμική άλγεβρα.
Γενικό μαθηματικό πρότυπο (πρότυπο προτύπων)
Τα στάδια ανάπτυξης ενός μαθηματικού κλάδου είναι:
1. Η επιλογή του βασικού υποκείμενου – συνόλου μελέτης.
2. Επιλογή των βασικών αξιωμάτων – βασικοί δομικοί κανόνες.
3.Κατασκευή.
4.Μορφισμοί: Βασικές απεικονίσεις που μεταφέρουν τις δομές ή τα βασικά δομικά στοιχεία.
5.Μετασχηματισμοί, ενδομορφισμοί και τα χαρακτηριστικά τους, αναλλοίωτα στοιχεία.
Η βασική τους πρόταση επομένως είναι η ανακάλυψη των αναλλοίωτων στοιχείων, διότι αυτά βοηθούν στην κατανόηση της δομής, στη μεταφορά της και κυρίως αποτελούν πυλώνες για το χτίσιμο ανάλογων δομών, όπως τα γλωσσικά καθολικά κατά Τσόμσκι. Σ’ αυτή τη φιλοσοφία θα μπορούσε να ενταχθεί και η μελέτη των παγκόσμιων χαρακτηριστικών στη μουσική, στον χορό, τη ζωγραφική και άλλες μορφές της ανθρώπινης δραστηριότητας.
Μουσικά καθολικά
H έρευνα για τα μουσικά καθολικά ξεκίνησε στις ΗΠΑ, κυρίως στο ΜΙΤ προφανώς και λόγω της ανάπτυξης των γλωσσικών καθολικών από τους γενετιστές του Τσόμσκι. Έκτοτε δημοσιεύτηκαν πλήθος μελέτες (Wachmann, 1971· Harwood, 1976· Lomax, 1977· Balkwill κ.ά., 1999· Brown, 2000· Mache, 2000· Brown κ.ά., 2000· Friedericki κ.ά., 2008). Φυσικά, δεν έλειψαν και οι αντίθετες στη θεωρία των καθολικών απόψεις, όπως αυτή του List (1971).
Συμφωνούμε με την άποψη που τίθεται από πολλούς ερευνητές ότι μάλλον πρόκειται για «σχεδόν καθολικά» (nearly universals), μιας και το απόλυτο δεν ισχύει στη φύση. Για παράδειγμα, όλοι οι άνθρωποι έχουν δύο χέρια, όμως υπάρχουν και άνθρωποι με ένα ή με κανένα χέρι. Όλοι οι άνθρωποι μιλάνε, όμως υπάρχουν και άνθρωποι που δεν μιλάνε και επικοινωνούν μέσω της νοηματικής γλώσσας.
Παραθέτουμε, λοιπόν, μερικά παραδείγματα καθολικών στη μουσική (universals in music) ή σχεδόν καθολικών (nearly universals), όπως αναφέραμε και παραπάνω:
◗ Βιμπράτο (Vibrato): Το βιμπράτο της φωνής προκαλεί έντονα συναισθήματα και συναισθηματική φόρτιση.
◗ Τραγούδια για παιδιά: Υπάρχει η τάση, όταν τραγουδάμε στα παιδιά, να τραγουδάμε σε υψηλότερες τονικότητεςσυχνότητες και με επαναληπτικότητα (γίνεται ακόμα και από κωφούς γονείς).
◗ Ακουστικά σχήματα-ακουστική φαντασία (auditory imagery): Η ικανότητα να φανταζόμαστε τη μουσική ακόμα και με την απουσία του ήχου.
◗ Τόνος και επιθετικότητα: H τάση να ακούμε τα χαμηλότερα τονικά ύψη ως πιο επιθετικά ή απειλητικά, ενώ τα υψηλότερα ως πιο ήρεμα ή υποχωρητικά. Γι’ αυτό το χαρακτηριστικό υπάρχουν δεδομένα και από το ζωικό βασίλειο.
◗ Χαμογελαστή φωνή: Tο χαμόγελο αλλάζει το ηχόχρωμα της φωνής κατά τέτοιον τρόπο ώστε ν’ ακούγεται πιο φιλική και λιγότερο απειλητική ή δεσποτική. Αυτό συμβαίνει επειδή η σύσπαση των μυών των παρειών μειώνει το άνοιγμα του στόματος και ανεβάζει τις συχνότητες όπως αναφέρθηκε πιο πάνω.
◗ Τραγούδια για παιδιά: Η γενική τάση για τα παιδικά τραγούδια είναι να τα λέμε δυνατά, προκειμένου να τραβήξουμε την προσοχή τους και με φωνή που σταδιακά ανεβαίνει.
Η δική μας προσέγγιση και έρευνα των μουσικών καθολικών μαζί με την Ελένη Βουγιουκλή, μουσικό-βαλκανιολόγο, θα μπορούσε να συνοψιστεί ως εξής:
◗ Ο ρυθμός. Η επαναληπτικότητα ενός ρυθμού στη μουσική με σκοπό την έκσταση, τον εξαγνισμό, την κάθαρση κ.ά.
◗ Το κοινό κίνητρο, αυτό της ανάγκης της έκφρασης. Δηλαδή, οι άνθρωποι δημιουργούν μουσική για να εκφραστούν και να επικοινωνήσουν.
◗ Η αφήγηση μύθων και ιστορίας των προγόνων. Γίνεται έτσι μεταφορά της πληροφορίας από γενιά σε γενιά.
◗ Οι ανάσες στο τραγούδι ως μέρος της μουσικής του ρυθμού.
◗ Καθολικά στοιχεία συναντάμε και σε δεύτερο επίπεδο, στο νόημα και τη θεματολογία του στίχου σε διαφορετική γλώσσα αλλά κοινά πανανθρώπινα θέματα: γέννηση, έρωτας, πόνος, πάθος, χαρά, ευτυχία, θρησκευτικές αναζητήσεις, απόρριψη, αρρώστια, θάνατος. Τελετουργικά τραγούδια, τραγούδια δηλαδή που συνδέονται με τον κύκλο της ζωής.
◗ Η αλληλουχία συγκεκριμένων αρμονιών που ακούγονται «όμορφα» και οικεία στο αυτί κάθε ανθρώπου, αυτές που ουσιαστικά αναφέρει ο Πυθαγόρας ως «συγγενείς ήχους», τις οποίες θα δούμε λίγο παρακάτω. Τέτοιο παράδειγμα είναι η αλληλουχία των συγχορδιών I-V-I (1η-5η-1η βαθμίδα) στην αρμονία, για όσους γνωρίζουν.
◗ Οι τρόποι χρήσης των φωνητικών χορδών, βλέπουμε, είναι κοινοί στους διαφόρους λαούς, φυσικά με κάποιες παραλλαγές. Μερικά παραδείγματα τρόπου χρήσης της φωνής είναι οι βοκαλισμοί, η πολυφωνία, το ομαδικό τραγούδι, ο συνεχής ήχος, τα «γυρίσματα», οι τρίλιες, οι αλαλαγμοί κ.ά.
◗ Οι τρόποι άντλησης έμπνευσης είναι κοινοί. Δηλαδή η προσπάθεια μίμησης ήχων του περιβάλλοντός μας όπως ο ήχος της γλώσσας, οι ήχοι των ζώων και της φύσης, του ανέμου, της ηχούς, της βροχής, της μουσικής και άλλα.
◗ Υπάρχουν κοινά χαρακτηριστικά στα μουσικά όργανα και στον τρόπο παραγωγής ήχου από τα μουσικά όργανα αυτά. Τα όργανα που συναντάμε στους διάφορους πολιτισμούς είναι είτε κρουστά, είτε πνευστά, είτε έγχορδα, είτε συνδυασμός αυτών των τριών. Το αρχέτυπο ενός πνευστού οργάνου όμως είναι ένα και είναι κοινό. Είναι ένας κύλινδρος, ένα καλάμι θα μπορούσαμε να πούμε, κούφιο κατά μήκος, ώστε να περνάει από μέσα ο αέρας και να δημιουργείται έτσι ένας ήχος. Από εκεί και πέρα, σε κάθε λαό συναντάμε παραλλαγές στο υλικό από το οποίο μπορεί να έχει φτιαχτεί αυτός ο αυλός, παραλλαγές στο μήκος του, τη διάμετρο, το είδος και τον αριθμό των οπών και πολλά άλλα. Παρομοίως και στα έγχορδα όργανα. Σε όλους του λαούς συναντάμε μια μορφή εγχόρδου (π.χ. λύρα, λαούτο, κιθάρα, μπάντζο, σιτάρ, άρπα κ.ο.κ.), του οποίου το αρχέτυπο είναι από μία μέχρι έναν οποιονδήποτε αριθμό χορδών, που ξεκινούν από ένα ηχείο και καταλήγουν σε έναν βραχίονα. Το υλικό, το σχήμα, το μέγεθος του ηχείου, του βραχίονα, των χορδών, το πλήθος των χορδών καθώς και ο τρόπος παιξίματος του κάθε οργάνου διαφέρει και ποικίλει από λαό σε λαό.
Αυτά είναι κάποια από τα βασικά καθολικά στοιχεία της μουσικής.
Τελευταίο όμως κρατήσαμε ένα από τα βασικότερα, κατά τη γνώμη μας, μουσικά καθολικά, μία από τις πιο σημαντικές κλίμακες της μουσικής, μία αρχέγονη κλίμακα που συναντάται σε όλους τους πολιτισμούς διαχρονικά: την πεντατονική κλίμακα.
Εδώ πρέπει να αναφέρουμε και τον γενικό ορισμό μιας μουσικής κλίμακας: Κλίμακα ονομάζουμε τη διάταξη διαδοχικών διαστημάτων στα πλαίσια μιας οκτάβας. Πεντατονικές κλίμακες συναντάμε στα ηπειρώτικα, στα ρεμπέτικα, στα μπλουζ, στα κινέζικα πολυφωνικά και όχι μόνο, στην ινδική μουσική, φυσικά στην αφρικανική μουσική, στην κάντρι (country), στη βραζιλιάνικη μουσική κ.ά.
Σε αυτό το σημείο θα θέλαμε να αναφερθούμε στον Πυθαγόρα και στους Πυθαγόρειους. Ο Πυθαγόρας και οι αρχαίοι ήξεραν φυσικά ότι το μήκος της χορδής είναι αντιστρόφως ανάλογο του τονικού ύψους του ήχου που παράγεται, δηλαδή της συχνότητας. Πίστη του ήταν όμως ότι υπάρχει ένας αριθμός, ο οποίος παράγει όλες τις νότες. Και αυτός ανακάλυψε ότι είναι ο 2/3, δηλαδή προσεγγιστικά η χρυσή τομή.
Πατώντας μια χορδή στα 2/3 του μήκους της, δίνει τον πιο συγγενή ήχο προς τον θεμέλιο (δηλαδή ολόκληρης της χορδής). Τα 2/3 του μήκους της χορδής παράγουν τα 3/2 του θεμέλιου ήχου, δηλαδή την πέμπτη της κλίμακας, δηλαδή το σημείο που ξεκινάει το χτίσιμο μια πεντατονικής κλίμακας.
Να επισημάνουμε ότι κατά την πρόσθεση των διαστημάτων κάνουμε πολλαπλασιασμό των λόγων και κατά την αφαίρεση, διαίρεση. Ακόμα, ότι οι λόγοι της χορδής ανεστραμμένοι εκφράζουν λόγους συχνοτήτων.
Για παράδειγμα, μπορούμε να πούμε ότι όταν πάλλονται τα 2/3 της χορδής – οπότε παράγεται ένα διάστημα πέμπτης καθαρής (διαπέντε) με την ανοικτή χορδή– η συχνότητα (τονικό ύψος) του νέου φθόγγου είναι 3/2 φορές μεγαλύτερη της συχνότητας της ανοικτής χορδής.
Βέβαια, σε κάποιες νότες οι τιμές διαφέρουν ελάχιστα με τον ήχο που παράγουν, υπάρχει δηλαδή μια μικρή απόκλιση. Θα μπορούσαμε να πούμε ότι ο ήχος-νότα είναι ένα ασαφές σύνολο (fuzzy). Κάτι που κατά τη γνώμη μας είναι πολύ σημαντικό και το οποίο αφορά και την αισθητική γενικότερα.
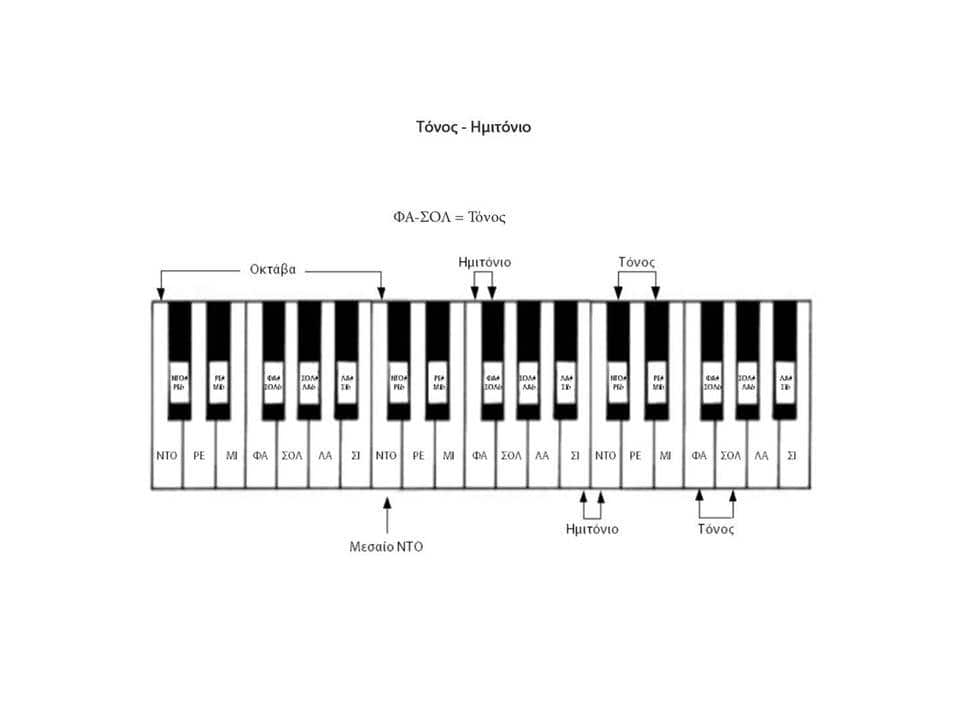
Ας πάρουμε για παράδειγμα τη νότα ΝΤΟ στη δυτική μουσική. Η αμέσως πιο κοντινή νότα στη ΝΤΟ είναι η ΝΤΟ#, ένα ημιτόνιο ψηλότερα, όπου ημιτόνιο είναι το μικρότερο διάστημα που υπάρχει στη δυτική μουσική.
Στη δυτική μουσική γραφή μεταξύ της νότας ΝΤΟ και της ΝΤΟ# ουσιαστικά δεν υπάρχει άλλη νότα. Στην πραγματικότητα όμως υπάρχουν άπειρες. Μπορούμε να παραλληλίσουμε και να προβάλουμε το παράδειγμα αυτό στα μαθηματικά, αν αντί για ΝΤΟ και ΝΤΟ# χρησιμοποιήσουμε τους αριθμούς 1 και 2 αντίστοιχα. Στο σύνολο των ακεραίων αριθμών δεν υπάρχει άλλος αριθμός μεταξύ των 1 και 2, αλλά στο σύνολο των πραγματικών αριθμών μεταξύ των αριθμών 1 και 2 υπάρχουν άπειροι αριθμοί. Έτσι και στη μουσική, μεταξύ των νοτών ΝΤΟ και ΝΤΟ# υπάρχουν άπειρες νότες, αλλά στη δυτική μουσική τουλάχιστον κατά σύμβαση επιλέγουμε το ημιτόνιο ως το μικρότερο διάστημα.
| ΝΤΟ | ΝΤΟ# | ΡΕ | |||
| Ι————… | …————Ι————… | …————Ι | |||
| ημιτόνιο | ημιτόνιο | ||||
Στην ινδική μουσική για παράδειγμα υπάρχουν πολύ πιο μικρές υποδιαιρέσεις της οκτάβας από τις δώδεκα υποδιαιρέσεις (ημιτόνια) της δυτικής μουσικής.
Και εδώ, μέσα από το συγκεκριμένο αυτό παράδειγμα προβολής της μουσικής στα μαθηματικά, θα μπορούσαμε να πούμε ότι προκύπτει αβίαστα η πρόταση να διδάσκονται οι δύο αυτές τέχνες μαζί, με τρόπο διαδραστικό. Να μην υπάρχει δηλαδή πλήρης διαχωρισμός τέχνης και επιστήμης. Πεποίθησή μας είναι ότι με αυτό τον τρόπο διευρύνονται οι ορίζοντες του μυαλού, απελευθερώνεται η σκέψη, αναπτύσσεται η φαντασία, καλλιεργείται η ολική αντίληψη των πραγμάτων εξοστρακίζοντας τη στενή και αποσπασματική αντιμετώπισή τους και έτσι εξελίσσεται η φιλοσοφία της ζωής.
Επίλογος
Μουσική και μαθηματικά, δύο παγκόσμιες γλώσσες επικοινωνίας, δύο τέχνες, δύο επιστήμες επαναστατικές που βρίσκονται σε μία αέναη αμφισβήτηση των υπαρχουσών δομών, θέτουν εκ νέου ερωτήματα, λειτουργούν ανατρεπτικά και «ενοχλητικά» απέναντι στη στασιμότητα και τον σκοταδισμό που κατά καιρούς ταλανίζει τον άνθρωπο. Υπηρετούν τον άνθρωπο και τις πραγματικές του ανάγκες και σπάνε τα εκάστοτε στεγανά ανά περιόδους, ανοίγοντας νέους δρόμους και προοπτικές για την κοινωνία και τον άνθρωπο. Συνοδεύουν και φωτίζουν την πρόοδο της σκέψης και του ψυχισμού. Οι δύο αυτές τέχνες λειτουργούν και πρέπει να λειτουργούν ως όχημα στην εξέλιξη του ανθρώπου και της κοινωνίας.
Βιβλιογραφία
Balkwill, L. L. & Thompson, W. F. (1999), «A crosscultural investigation of the perception of emotion in music: Psychophysical and cultural cues», Music Perception 17: 43–64.
Blacking, J. (1977), «Can musical universals be heard?», The World of Music 19: 14–22.
Brown, S. (2000), «The “musilanguage” model of music evolution» στο S. Brown, B. Merker, N.L. Wallin (επιμ.). The origins of music: 271–300, MIT press: Massachusetts.
Chomsky, N. (1965), Aspects of the Theory of Syntax, MIT Press: Massachusetts.
Cross, I. & Morley, I. (2008), The evolution of music: Theories, definitions and the nature of the evidence. Communicative musicality: 61–82. Oxford University Press: Oxford.
Good, J. (επιμ.) (2008), Linguistic universals and language change, Oxford University Press: Oxford.
Harwood, D. L. (1976), «Universals in music: A perspective from cognitive psychology», Ethnomusicology 20: 521–533.
List, G. (1971), «On the non-universality of musical perspectives», Ethnomusicology 15: 399–400.
Lomax, A. (1977), «Universals in song», The World of Music 19: 117–129.
Mâche, F. B. (2000), The necessity of and problems with a universal musicology, The origins of music: 473–479, MIT Press: Massachusetts.
Mâche, F. B. (2000), «The necessity of and problems with a universal musicology» στο S. Brown, B. Merker & N. L. Wallin (επιμ.). The origins of music: 473–479, MIT Press: Massachusetts.
Friederici, A. D., Knösche, T. R., Nan, Y. & Syosset, S. (2008), «Cross-cultural music phrase processing: An fMRI study», Human Brain Mapping 29: 312–328.
Vougiouklis, T. & Kambaki, P. (2008), «Algebraic Models in Applied Research», Jordan Journal of Math and Statistics 1(1): 78-87.
Wachsmann, K. P. (1971), «Universal perspectives in music», Ethnomusicology 15: 381–384.
Brown, S., Merker, B. & Wallin, N.L. (επιμ.) (2000), The origins of music, MIT Press: Massachusetts.
Wells, S. (2007), Deep ancestry: Inside the genographic project, National Geographic: Washington DC.
Βάζου, Ε., Ξυδόπουλος Γ. Ι., Παπαδοπούλου Φ. & Τσαγγαλίδης Α. (2008), Εισαγωγή στη μελέτη της γλώσσας, Πατάκης: Αθήνα.
Βουγιουκλής, Θ. & Καμπάκη, Π. (2002), «Απλά» μαθηματικά μοντέλα στη γλώσσα, 19o Παν. Συν. Μαθ. Παιδείας ΕΜΕ, Κομοτηνή, 506-515.
Δημητρίου, Σ. (1983), Λεξικό Όρων Γλωσσολογίας, τόμ. Α’, Β’, Καστανιώτης: Αθήνα.
Καμπάκη–Βουγιουκλή, Π. (2008), Εισαγωγικά μαθήματα γλωσσολογίας κατά παράδοση, Σπανίδης: Ξάνθη.
Καμπάκη–Βουγιουκλή, Π. (2009), Γλώσσα και μαθηματικά πρότυπα, Αδελφοί Κυριακίδη: Θεσσαλονίκη.
Παυλίδου, Θ. (1995), Επίπεδα γλωσσικής ανάλυσης, Παρατηρητής: Θεσσαλονίκη.